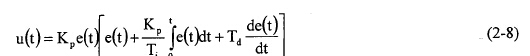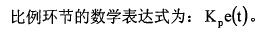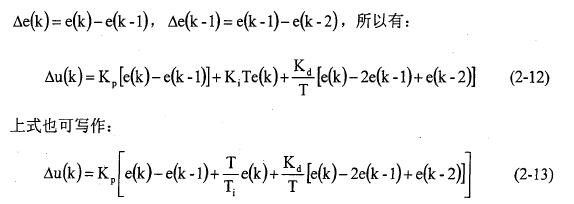PID控制方法是經(jīng)典控制算法中的典型代表,與模糊控制結(jié)合,能夠更好的發(fā)揮其優(yōu)勢(shì)�。PD控制是**早發(fā)展起來的控制策略之一,具有魯棒性好、可靠性高和結(jié)構(gòu)簡(jiǎn)單的特點(diǎn),適用面很廣�。PID控制器及其改進(jìn)型是在工業(yè)過程控制中**常見的控制器。據(jù)統(tǒng)計(jì),工業(yè)控制的控制器中Pro類占有90%以上�。然而實(shí)際被控對(duì)象或過程往往難以建立精確的數(shù)學(xué)模型,具有非線性、時(shí)變不確定性,使用常規(guī)的PD控制算法不能得到理想的控制效果�����。智能控制理論的發(fā)展和計(jì)算機(jī)技術(shù)為解決復(fù)雜動(dòng)態(tài)不確定系統(tǒng)的控制提供了新途徑,也為PID的改進(jìn)開辟了新空間��。
IP功控制的發(fā)展
Pro的發(fā)展過程,實(shí)質(zhì)上是參數(shù)自適應(yīng)和參數(shù)整定方法的研究過程��。[,91PID參數(shù)整定方法shou先由Ziegler和Nichols提出,之后許多技術(shù)被用于PID控制器的手動(dòng)和自動(dòng)整定�。PD參數(shù)整定方法有多種劃分方式。按發(fā)展階段,劃分為常規(guī)PID參數(shù)整定方法和智能PD參數(shù)整定方法;按控制量形式的組合,劃分為非線性PID參數(shù)整定方法和線性PID參數(shù)整定方法,前者用于由非線性跟蹤微分器和非線性組合方式生成的非線性PID控制器,后者用于經(jīng)典PID調(diào)節(jié)器;按被控對(duì)象的多少`,劃分為多變量Pro參數(shù)整定方法和單變量PD參數(shù)整定方法,前者是**近研究的難點(diǎn)及熱點(diǎn),后者囊括了現(xiàn)有的大多數(shù)整定方法�。
智能PD參數(shù)整定方法包括基于規(guī)則的自整定方法和基于模型的自整定方法?����;谀P偷淖哉ǚ椒ㄊ峭ㄟ^頻率響應(yīng)實(shí)驗(yàn)、參數(shù)估計(jì)及暫態(tài)響應(yīng)實(shí)驗(yàn)來獲取過程模型����。基于規(guī)則的自整定方法的整定是基于類似有經(jīng)驗(yàn)操作者手動(dòng)整定的規(guī)則,不用獲得過程實(shí)驗(yàn)?zāi)P?����。與基于模型的自整定方法一樣,基于規(guī)則的自整定方法使用負(fù)載干擾���、暫態(tài)響應(yīng)或設(shè)定值改變等信息,對(duì)被控過程的特性觀測(cè)�����。若被控量與設(shè)定值不符,則控制器參數(shù)進(jìn)行基于規(guī)則整定。一般通過對(duì)響應(yīng)特性進(jìn)行量化,來獲得一個(gè)基于規(guī)則的自整定過程�����。通常使用的量是描述控制回路響應(yīng)速度的時(shí)間常數(shù)和振蕩頻率,以及用來描述控制系統(tǒng)穩(wěn)定性的超調(diào)量和衰減比��。獲得決定不同控制器參數(shù)的相應(yīng)規(guī)則應(yīng)該增加或減少相對(duì)比較容易,但確定增減的量困難比較大�。因此,連續(xù)自適應(yīng)控制一般使用基于規(guī)則的整定方法�����。設(shè)定值變化的控制通常使用基于模型的整定方法,而在處理負(fù)載干擾和處理設(shè)定值變化的對(duì)象時(shí)基于規(guī)則的整定方法采用的處理方式相同���。
從目前PD參數(shù)整定方法的研究和應(yīng)用現(xiàn)狀來看,今后的發(fā)展過程中研究和實(shí)踐的重點(diǎn)和發(fā)展方向主要體現(xiàn)在以下幾個(gè)方面:
(l)對(duì)于單輸入單輸出被控對(duì)象,需要進(jìn)一步研究PID參數(shù)整定方法,針對(duì)不穩(wěn)定被控過程或?qū)ο蟠嬖谳^大干擾的情況,增強(qiáng)在初始化和魯棒性等方面的性能,盡量使用的操作簡(jiǎn)單且過程信息少,就可以很好的完成整定。
(2)對(duì)于多輸入多輸出被控對(duì)象,需要對(duì)多變量PD參數(shù)整定方法研究,針對(duì)多變量過程的顯著藕合關(guān)系,使分散繼電反饋方法進(jìn)一步完善,使用到的先驗(yàn)信息量盡可能減少,易于在線整定�。
(3)有待進(jìn)一步研究智能PD控制方法和應(yīng)用,將增益計(jì)劃設(shè)定和自適應(yīng)、自整定二者有機(jī)結(jié)合,使其增加自動(dòng)診斷功能;對(duì)原有工控制器設(shè)計(jì)思想及整定方法進(jìn)行改進(jìn),結(jié)合**經(jīng)驗(yàn)知識(shí)��、直覺推理邏輯等**系統(tǒng)思想和方法;為進(jìn)一步提高控制系統(tǒng)性能,將PD控制�����、模糊控制和預(yù)測(cè)控制交叉應(yīng)用����。以上都是智能控制發(fā)展很有前途的*域。
ZP功控制的原理
PD控制器是將偏差的比例P�����、積分I�����、微分D線性并聯(lián)組合的控制器[20]。
其數(shù)學(xué)模型可以用下式表示:
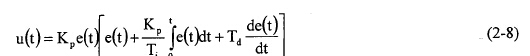
其中:e(t)—控制器的輸入,是被控對(duì)象輸出量和設(shè)定目標(biāo)量的偏差信號(hào)
Ti—控制器的積分時(shí)間
KP—控制器的比例系數(shù)
Td—控制器的微分時(shí)間
u(t)—控制器的輸出
式(2一8)表明比例���、積分�����、微分三個(gè)校正環(huán)節(jié)構(gòu)成了PID控制器的數(shù)學(xué)模型���。
(l)t匕例環(huán)節(jié)。
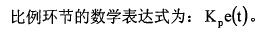
從數(shù)學(xué)表達(dá)式可知,積分環(huán)節(jié)的調(diào)節(jié)作用與偏差的積分成正比��。不管存在偏差的大小,控制作用都會(huì)隨時(shí)間的增加而不斷增大�����。只有當(dāng)偏差e(t)為o時(shí),積分常數(shù)才為O,這時(shí)該部分不具有控制作用���?����?梢?積分環(huán)節(jié)的作用是將系統(tǒng)的穩(wěn)態(tài)誤差消除。積分環(huán)節(jié)的作用受積分時(shí)間工的影響很大。當(dāng)工較小時(shí),積分有較強(qiáng)的作用,則系統(tǒng)過渡過程中有可能產(chǎn)生的超調(diào)較大,但只需較短的時(shí)間就可消除偏差;當(dāng)工較大時(shí),積分有較弱的作用,則系統(tǒng)過渡過程中不易產(chǎn)生超調(diào),但是需要較長(zhǎng)的時(shí)間消除偏差����。因此,調(diào)節(jié)過程的初期,積分應(yīng)當(dāng)弱一些,甚**可以取零,之后應(yīng)增強(qiáng)積分作用,有利于消除穩(wěn)態(tài)誤差。
(3)微分環(huán)節(jié)
從數(shù)學(xué)表達(dá)式可知`,微分環(huán)節(jié)的調(diào)節(jié)作用與被調(diào)量的變化率成正比�。微分時(shí)間幾對(duì)微分環(huán)節(jié)的作用影響很大。幾越小,則抑制e(t)變化的作用越弱;幾越大,則抑制e(t)變化的作用越強(qiáng)����。可見,微分環(huán)節(jié)很大程度上影響系統(tǒng)的穩(wěn)定����。
但幾過小,調(diào)節(jié)過程制動(dòng)落后,導(dǎo)致增大超調(diào);幾過大,調(diào)節(jié)過程制動(dòng)超前,致使調(diào)節(jié)時(shí)間過長(zhǎng)。所以在調(diào)節(jié)過程前期,應(yīng)加大微分的作用;臨近穩(wěn)態(tài)時(shí),減小微分的作用,加快響應(yīng)速度����。
如果控制系統(tǒng)的硬件設(shè)計(jì)以微處理器為核心,那么該控制系統(tǒng)就是時(shí)間離散的控制系統(tǒng),它以采樣頻率對(duì)輸入和輸出量進(jìn)行實(shí)時(shí)采樣,所以PID控制器采用差分方程表示: